Logic: proving the valid syllogisms

introduction

Added later: there is an Edit near the very end; I removed some silly text.

In this post I want to “finish off” syllogisms. No, this is certainly not the last word on syllogisms, and is almost certainly not my last word on them… but when I pick them up next, it will probably be to look at them using Boolean algebra.

What I propose to do in this post is

• prove the four valid syllogisms in figure 1;
• reduce the number of essentially distinct valid syllogisms from 15 to 8;
• reduce that number from 8 to 6;
• prove the two additional valid syllogisms;
• suggest practical guidelines.

Let me begin by summarizing some of the information we will need to have at our fingertips.

Logic: adding and dropping quantifiers

Introduction

In this post, I want to introduce us to the formalism of adding or removing quantifiers.

Let me say up front that what I’m about to do amounts to parking my car at a “vista point” along the road, and looking around. If I accomplish anything in this post, it may be to give us some background and context for taking a course in formal symbolic logic, or for working carefully through a text.

As we have seen before, in three or four of my logic posts, there are two quantifiers, 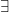 and ; they are read “there exists ” and “for all”. The first is called “the existential quantifier” and the second is called “the universal quantifier”. It seems that this material was first devised independently by Gentzen and Jaskowski in 1934, so it is surprisngly recent in logic.

What we want to do is to move comfortably between truth tables and tautologies and rules of inference, which do not contain quantifiers… and the kinds of statements which do contain quantifiers, which we find in mathematics and classical logic.

I will be using material I’ve posted about rules of inference and tautologies in one post, “all” and “some” in a second post, and syllogisms in a third prior post.

We have two quantifiers, and two operations to apply to each, so we should expect to find four rules.

Two of these laws remove quantifiers, and two of them add quantifiers. Their precise statements are covered with barbed wire; let’s begin with relatively vague statements. To put that another way, let’s start by being as vague as people usually are when they use these rules.

“The goal is not to make you a mathematical logician; the goal is to make you comfortable enough with quantifiers.” Exner, p. 68.