happenings – 31 May

Not much. I’m down with a cold, and don’t feel at all energetic or like focusing on anything.

Sure, I’m browsing “simplicial complexes” in books other than Bloch: his treatment is a little too condensed for me, and I want to play with those things. And I’m thinking about PCA / FA as Malinowski does it, but he has broken out of the box we’ve been in, in a couple of ways, and I’m struggling with the presentation (FYI, “target testing”, and “noise”).

But mostly I’m sneezing my way thru a roll of paper towels, sitting in a recliner in front of the TV. Oh, right now I’m heating up a medium pot of chicken soup, and putting this out while I stay close to the stove.

I’ll put out some math when I’m up to it.

the matrix exponential: 3 of 3

discussion

There was a lot going on in the example of the SN decomposition (2 of 3). First off, we found eigenvalues of a non-diagonable matrix A, and constructed a diagonal matrix D from them. Then we found 2 eigenvectors and 1 generalized eigenvector of A, and used them to construct a transition matrix P. We used that transition matrix to go from our diagonal D back to the original basis, and find S similar to D.

So S is diagonable while A is not. And A and S have the same eigenvalues; and the columns of P should be eigenvectors of S. They are. The generalized eigenvector that we found for A is an (ordinary) eigenvector of S, but we had to get a generalized eigenvector of A in order to construct S from D.

I wonder. Can I understand the distinction between eigenvectors and generalized eigenvectors by studying S and A? We’ll see.

the matrix exponential: 2 of 3

let’s look at an example of the SN decomposition.

This comes from Perko p. 35, example 3. We will compute exp(A) using the SN decomposition described in the previous post (“1 of 3”).

We take the following matrix:

I ask Mathematica® to find its eigenvalues and eigenvectors. For eigenvalues, I get

For the eigenvector matrix, I get

the matrix exponential: 1 of 3

discussion

one correction 30 Aug 2008, per Brian Hall’s comment and counterexample here. see “edit” in this post.

Let me emphasize something I take for granted: i’m writing about theory as opposed to computations by computer. every time I say, for example, that two matrices A and B are similar via

,

I am asserting that P is a transition matrix for a change-of-basis, and by definition it is invertible. In practice, the matrix P can be ill-conditioned, and computing on a computer may be extremely hazardous.

An updated version of a classic paper may be found here . Having just looked at it, I may pepper my theoretical discussion with some vaguely computational comments.

Back to my ivory tower. Well, it’s hardly that, but it’s still far removed from numerical algorithms.

The definition of the matrix exponential is easy enough to write: as the exponential of a number x has the expansion

we define

But how do we actually compute it (in theory)? Well, we could just try computing the powers of A and look for a pattern, but there are easier ways. Far easier ways. (and just doing it numerically can be a bad idea: we can encounter disastrous cancellation between one power of A and the next.)

books added – 25 May

References for generalized eigenvectors, the matrix exponential and for the SN decomposition.

one correction 30 Aug 2008, per Brian Hall’s comment below. see “edit” in this post.

First, let’s talk about books which are already in the bibliography. It’s pretty easy to find statements that for matrix exponentials,

exp(A+B) = exp(A) exp(B)

Topological Surfaces: Bloch Ch 2.

Let me talk about the second chapter, “Topological Surfaces” in Bloch’s “A First Course in Geometric Topology and Differential Geometry”. I finished it quite a while ago, but I’ve had trouble deciding how to talk about it. I don’t want to just summarize it. Instead, I think I’ll try asking and answering some leading questions.

First of all, why did I choose to read Bloch? A few years ago, I was seriously shaken up by the following, from Freed & Uhlenbeck’s “Instantons and Four-Manifolds”, p. 1: “A basic problem is to ascertain when a topological manifold admits a PL [piecewise linear] structure and, if it does, whether there is also a compatible smooth [differential] structure. By the early 1950’s it was known that every topological manifold of dimension less than or equal to three admits a unique smooth structure.” They were setting us up for the fact that it isn’t generally true in dimensions greater than 3.

To be explicit about the challenge we face: topological, simplicial (which Bloch tells me generalizes to PL), and differential structures on a manifold coincide for low dimensions but not for high, and “high” means “greater than 3”.

This was all news to me. I knew, for a small value of knew, differential geometry, and I’d seen some simplicial stuff – triangulating and cutting up surfaces – and I was acquainted with topology, possibly for a large value of acquainted, but their “basic problem” was nothing I’d ever heard before.

Corrections

So far, there are only two that I know of. One is here in “attitude & transition matrices”; the other is here in “the SVD generalizes eigenstructure”.

I was reading yet another book on PCA / FA last night, and I came across a definition saying that two matrices A and B were similar if. Of course, I objected that P needed to be orthogonal, and we couldn’t guarantee that in general. This morning, out with one of the cats – and, therefore, thinking instead of computing or writing! – I observed that the author had made that mistake because the matrices 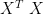and 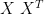are symmetric, and for symmetric matrices it is certainly true that P may be chosen orthogonal. He had been careless because within the realm of PCA / FA, we are only finding eigendecompositions of symmetric matrices. Within the realm of PCA / FA, we may take P to be orthogonal, because we’re looking at 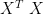and/or 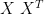when we’re not using the SVD.

It was a while after that I began to wonder if I had made the very same mistake.

I had. Damn!

I have corrected it. It was in among the SVD posts, specifically “the SVD generalizes eigenstructure”. if someone else had written my post, I think I would have caught that. Unfortunately, when I read my own stuff, I sometimes read what I meant to write, instead of what I did write. (That’s how I learned to let another grad student take a test before I handed it out to my students. He’d have to read what I wrote; take it myself, and I don’t even stop to read the questions!)

As I said, if A is symmetric, we may choose P orthogonal. More generally, if A is hermitian, we may choose P unitary. In ultimate generality, we may choose P unitary if and only if A is normal.

I have even shown you that we cannot always have P unitary. The counterexample in the schur’s lemma post was specifically a non-normal matrix which could be diagonalized, but whose eigenvectors were not orthogonal, i.e. whose eigenvector matrix was not, and could not be made, unitary.

FWIW, for any 3D rotation matrix – which is orthogonal, hence normal – we may choose P unitary but not orthogonal: even though the rotation matrix is real, its eigenvector matrix is complex and can only be made unitary.

Quantum Mechanics and rotations

Let me warn you up front that I cannot yet reconcile Feynman’s answers with McMahon’s recipe. Well, this is supposed to be about the doing of math, not just about math itself.

For Feynman, i’m in “Lectures on Physics”, volume III, Quantum Mechanics. For McMahon, i’m using “Quantum Mechanics Demystified.” References to Schiff are to his “Quantum Mechanics”.

We have looked at the following here: if I know that a spin-1 particle is in the Jz state |+>, i.e.

and I wanted to know: what are possible values of Jx (the x-component of angular momentum)? and with what probabilities would they occur? What we looked at was the relationship between Jz and Jx in a given coordinate system

I want to consider a different question; I want to rotate the coordinate system.

axis and angle of rotation

edit: I have solved the problem of the sign ambiguity. see 28 Sept 2008.

I was going to call this “rotations 2”, but I decided to put the key computations in the name.

from rotation matrix to axis and angle of rotation

Having gotten the rotation (attitude) matrix for mars coordinates here, can we find its axis of rotation? (not of mars, of the attitude matrix!)

Sure, that’s just the eigenvector with eigenvalue 1!

Every 3D rotation has an eigenvalue of 1: there is a line in space which is left fixed under the rotation. Any vector on that line is an eigenvector. It has eigenvalue 1 because the line is not being stretched or compressed: nothing has been done to it. The other two eigenvalues are complex, and so are their eigenvectors, because there are no other subspaces which are left fixed by the rotation.

When I ask Mathematica® to find the eigenvalues and eigenvectors of the mars rotation matrix, the eigenvector with eigenvalue 1 is:

That’s very nearly the z-axis, as it should be.

There’s just one little problem. The negative of that eigenvector – the negative z-axis – is every bit as good an answer. Any multiple of it is every bit as good an answer. We know the rotation axis, but we don’t know the direction of it. What we really know is the line in space which is left fixed by the rotation.

rotations 1

here, have some rotations

Let us suppose that someone hands us these three rotation matrices about the z, y, and x axes respectively.

around the z-axis

Now, just what are they? Better, what do they do to vectors?

Answer: viewed as active transformations (“alibi”), they do CW rotations of vectors. The keys: active transformation, CW.

Alternatively, viewed as passive transformations (“alias”), they are attitude matrices for CCW rotations of coordinate axes. There are three keys to that answer: passive transformation, CCW, and attitude matrix. (in more general cases, one of which I will look at below, they are inverse transition matrices instead of attitude matrices.)