PCA / FA. Example 4 ! Davis, and almost everyone else

I would like to revisit the work we did in Davis (example 4). For one thing, I did a lot of calculations with that example, and despite the compare-and-contrast posts towards the end, I fear it may be difficult to sort out what I finally came to.

In addition, my notation has settled down a bit since then, and I would like to recast the work using my current notation.

The original (“raw”) data for example 4 was (p. 502, and columns are variables):

PCA / FA example 4: davis. Summary.

Considering how much I learned from Davis’ little example, I almost hate to summarize it. The following just does not do justice to it. We’ll see if the passage of time – coming back to Davis with fresh eyes after doing the next example – improves the summary.

OTOH, an awful lot of what I got out of Davis came from bringing linear algebra to it, and just plain mucking about with the matrices. And I discovered, having picked up the two chemistry books since I drafted this post, that they made a lot more sense than when I first looked at them. I have learned a lot from working with Davis’ example.

Here’s what I have. My own strong preference, but I’d call it a personal choice, is to use the SVD of the data matrix X:

and compute the A’s and S’s (R-mode and Q-mode loadings and scores):

.

.

.

.

Those equations are worth having as a conceptual basis even if one chooses to do eigendecompositions of or instead of the SVD.

PCA / FA example 4: davis. Davis & Jolliffe.

What tools did jolliffe give us (that i could confirm)?

1. Z = X A, A orthogonal, X old data variables in columns
2. serious rounding
3. plot data wrt first two PCs
4. how many variables to keep?

but jolliffe would have used the correlation matrix. Before we do anything else, let’s get the correlation matrix for davis’ example. Recall the centered data X:

i compute its correlation matrix:

Now get an eigendecomposition of the correlation matrix; i called the eigenvalues and the eigenvector matrix A. Here’s A:

If we compute and get an identity matrix, then A is orthogonal. (it is.)

PCA / FA example 4: davis. Reciprocal basis 4.

(this has nothing to do with the covariance matrix of X; we’re back with for the SVD of X.)

in the course of computing the reciprocal basis for my cut down

i came up with the following matrix:

now, is very well behaved. Its two columns are orthogonal to each other:

PCA / FA example 4: davis. Davis & harman 3.

Hey, since we have the reciprocal basis, we can project onto it to get the components wrt the basis. After all that work to show that the are the components wrt the reciprocal basis, we ought to find the components wrt the basis. And now we know that that’s just a projection onto the reciprocal basis: we want to compute X B.

Recall X:

Recall B:

The product is:

What are the column variances?

Does that surprise you?

PCA / FA example 4: davis. Reciprocal basis 2 & 3.

The reciprocal basis for A^R using explicit bases.

Here I go again, realizing that I’m being sloppy. i call

the second data vector, but of course, those are the components of the second data vector. a lot of us blur this distinction a lot of the time, between a vector and its components. So long as we work only with components, this isn’t an issue, but we’re about to write vectors. i wouldn’t go so far as to say that the whole point of matrix algebra is to let us blur that distinction, but it’s certainly a major reason why we do matrix algebra. but for now, let’s look at the linear algebra, distinquishing between vectors and their components.

i need a name for the second data vector; let’s call it s. we will write it two ways, with respect to two bases, and show that the two ways are equivalent.

PCA / FA example 4: davis. Scores & reciprocal basis 1.

The reciprocal basis for , using matrix multiplication.

i keep emphasizing that is the new data wrt the orthogonal eigenvector matrix; and i hope i’ve said that the R-mode scores are not the new data wrt the weighted eigenvector matrix . In a very real sense, the R-mode scores do not correspond to the R-mode loadings . This is important enough that i want to work out the linear algebra. In fact, i’ll work it out thrice. (And i’m going to do it differently from the original demonstration that is the new data wrt v.)

Of course, people will expect us compute the scores , and I’ll be perfectly happy to. I just won’t let anyone tell me they correspond to the .

First off, we have been viewing the original data as vectors wrt an orthonormal basis. Recall the design matrix:

Let’s take just the second observation:

Those are the components of a vector.

PCA / FA example 4: davis. Davis & harman 2.

What about redistributing the variance?

We learned from harman that if we use the orthogonal eigenvector matrix v to compute new data, the result has redistributed the original variance according to the eigenvalues; and we also learned that if we use the weighted eigenvector matrix instead, we get new variables of unit variance.

(i think i thought this required us to start with the correlation matrix; it does not.)

let’s see this again for davis’ centered data X:

We have variances…

or…

and the sum of the variances is…

32.

PCA / FA example 4: davis. Davis & harman 1.

Let us now recall what we saw harman do. Does he have anything to add to what we saw davis do? if we’re building a toolbox for PCA / FA, we need to see if harman gave us any additional tools.

here’s what harman did or got us to do:

• a plot of old variables in terms of the first two new ones
• redistribute the variance of the original variables
• his model, written Z = A F, was (old data, variables in rows) = (some eigenvector matrix) x (new data)

We should remind ourselves, however, that harman used an eigendecomposition of the correlation matrix; and the eigenvectors of the correlation matrix are not linearly related to the eigenvectors of the covariance matrix (or, equivalently, of 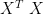.) having said that, i’m going to go ahead and apply harman’s tools to the davis results. i will work from the correlation matrix when we get to jolliffe.

What exactly was that graph of harman’s? he took the first two columns of the weighted eigenvector matrix, then plotted each row as a point. He had 5 original variables. His plot

shows that the old 1st and 3rd variables, for example, are defined very similarly in terms of the first two new variables. let me emphasize that this is a description of defining variables, not a display of the resulting data. Simple counting can help with the distinction, e.g. 3 variables but 4 observations.

PCA / FA example 4: Davis review (3)

Let’s talk about centering the data. Recall the questions:

• is there any chance that we can always center both the columns and the rows?
• is there any chance that we can always standardize both the columns and the rows?
• if we can’t have our cake and eat it too, should we give up the duality between R-mode and Q-mode?
• what if rows of the data matrix add up to 1 or 100 (i.e. the variables are percentages)?

(My third question is poorly phrased. we always have the duality between A’s and S’s; what i feared losing was the idea that Q-mode is just R-mode applied to the transpose ; but what if X doesn’t have row-centered data?)

The third question is also a red herring. We can always make both the columns and the rows add up to zero. Proving it isn’t too hard; some convenient notation might simplify things. If the data is

then

and

are good symbols for the column means and row means, respectively. The grand mean (the mean of all the matrix values = mean of column means = mean of row means) would be denoted